I am broadly interested by all topics related to energy and nanotechnology/nanoscience. I have been especially dealing with nanoscale thermal radiation and nanoscale heat conduction, and their connection to energy conversion.
Nanoscale (ballistic) heat conduction
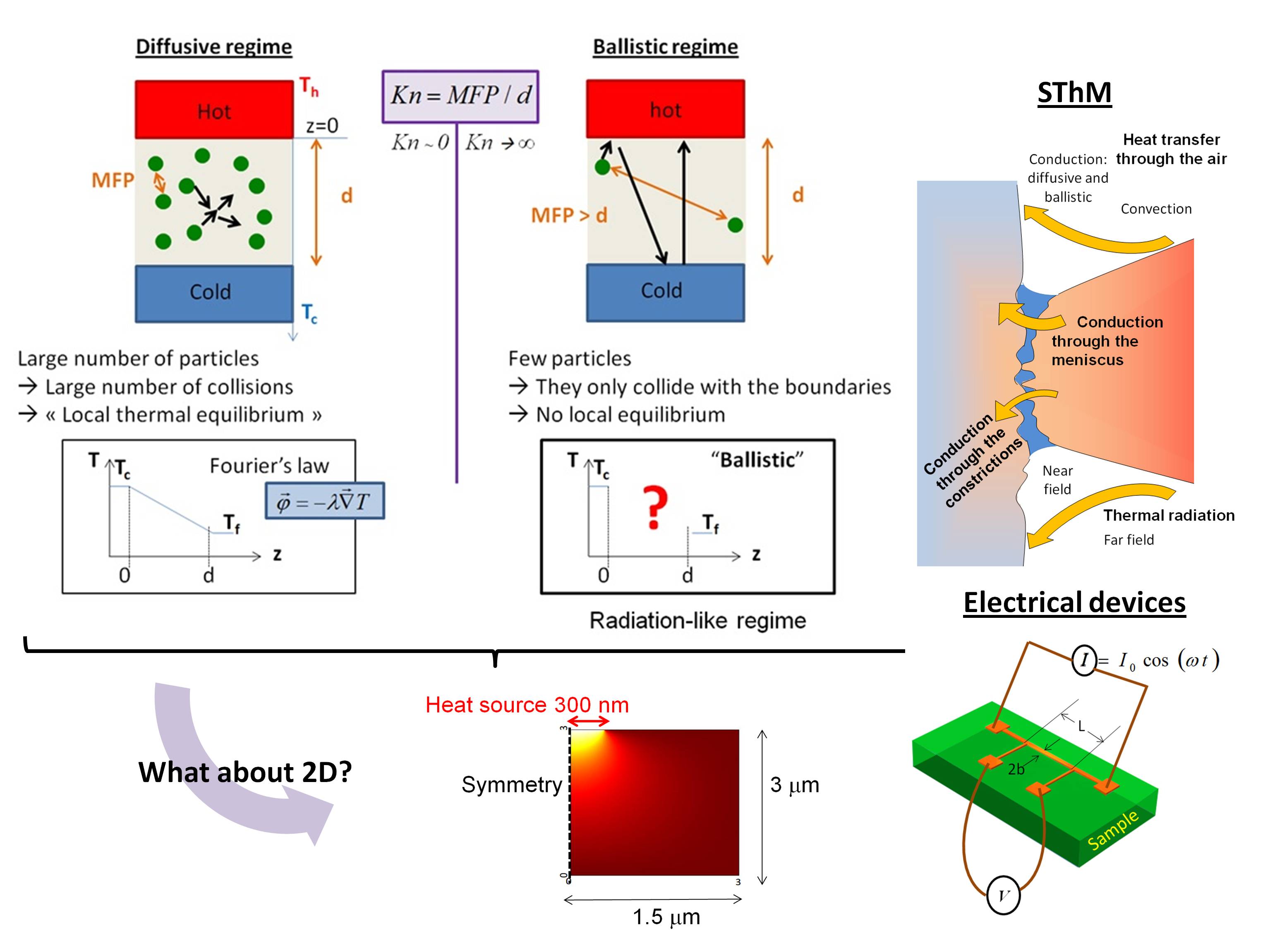
In electrically-insulating solids or in semiconductors, heat is mainly transferred by phonons. I have been interested by many aspects related to these energy carriers, in particular by the impact of the confinement of their sources (Paris, Barcelona). The analysis can be performed in light of the Boltzmann transport equation for phonons. A particularly-interesting way to analyse heat conduction from a localized heat source is scanning thermal microscopy (see review), a technique for localized thermal probing. We are actively moving toward complex thermal confinement such as two-dimensional one, taking advantage of the progresses that have been made in the last decade in the simple configurations (nanowires, velocities and relaxation times can be measured for a (low-frequency...) portion of the spectrum and compared to acoustic calculations.
We are pursuing this phononic approach (see our paper on phononic resistances). It is especially tempting to analyze these aspects in light of the non-linearities that could take place: they may lead to thermal rectification, which is at the heart of the dreams of a future revolution linked to the mastering of energy in solids.
Link to a basic presentation on heat conduction at nanoscale (in French, no wave regime).
Microscale and nanoscale (sub-wavelength) thermal radiation
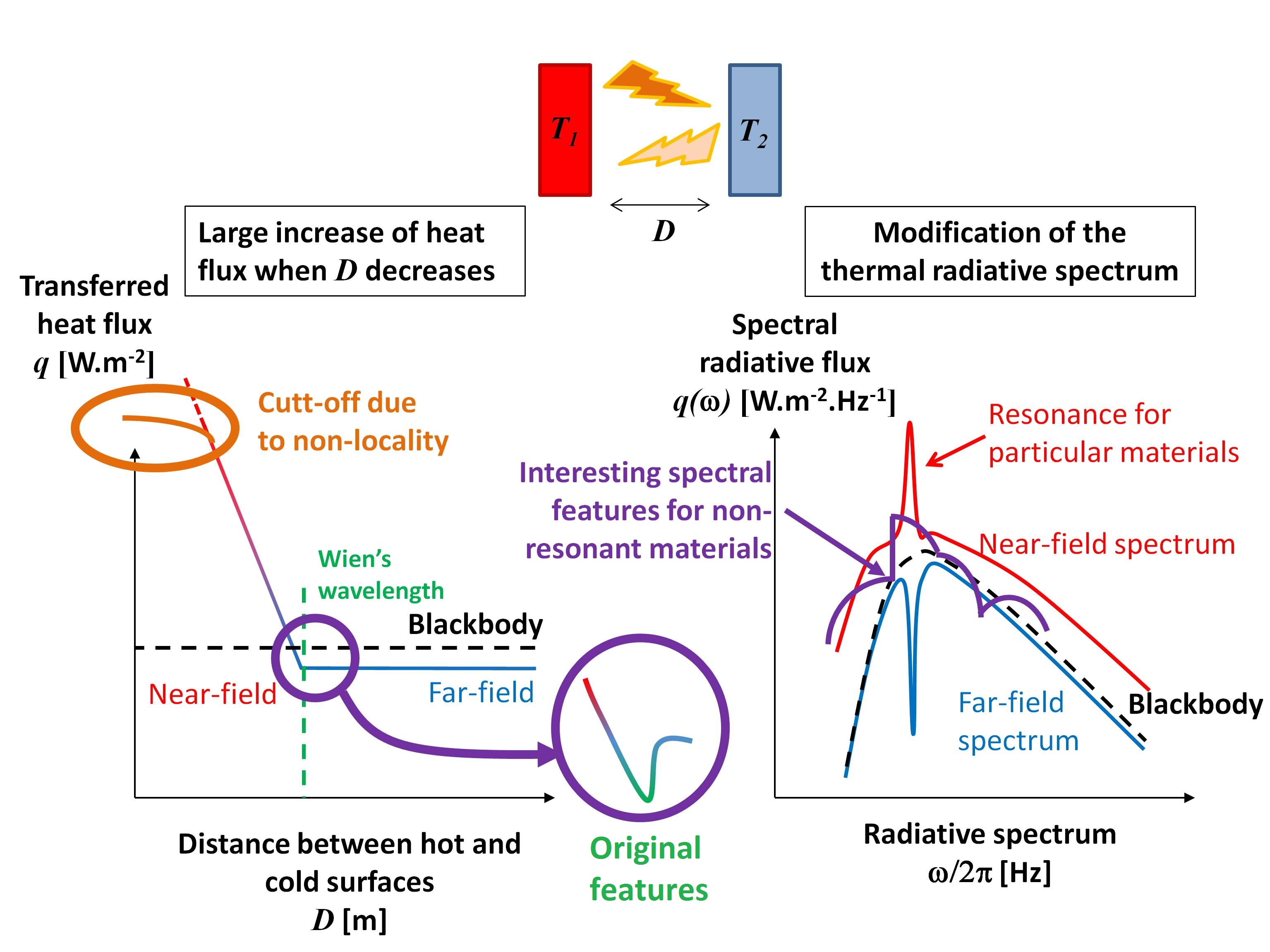
Since a decade, rigorous experiments are possible: the most striking ones have been those in Germany, at MIT (1, 2), in France, in Florida, and in the Czech Republic. In addition to the early preparation of an experiment, I have been involved in the analysis of the experiments dealing with metals, and especially at the limits of fluctuating electrodynamics (spatial non-locality). More recently, information related to the thermal spectra in the near field has been observed (Paris 1&2, Boulder). It is extremely interesting that the spectrum of thermal radiation can change and exhibit peaks where a lot of energy is confined (as predicted by Greffet et al.).
We have recently analyzed the prediction of possible decreases of the heat exchanged by radiating surfaces below the far-field limit for bulk surfaces (see our article and the work by colleagues at Columbia University) and thin films. This is due to the existence of a coherent regime which can start at much larger distances than what was thought previously (link). Thin films and finite objects are also interesting due to their far-field thermal radiation properties which differ from the macroscopic ones and can be optimized.
Link to a basic presentation on thermal radiation at micro and nanoscale (in French).
Nanoscale energy conversion

Among these sources one can find thermoelectricity, the goal of which is to generate electricity from a difference of temperature between two close locations. Peltier and Seebeck are credited with the main discoveries linked to thermoelectricity. Since it was shown that thermal insulation is required for such phenomenon to to take place, nanoscale design is exploited to improve the associated devices.
Another possible way to harvest energy is thermophotovoltaics, which was proposed in particular by Kolm and Aigrain in the 1950s-1960s. This is parallel to photovoltaics, but the sources are radiating bodies at intermediate (~800°C) or high temperature (~1500°C) instead of the sun directly, which leads to constraints for the radiating bodies (see e.g. some of them). Various options allow overcoming the flux limitation due to blackbody radiation. The first one is near-field thermophotovoltaics, where one can take advantage of the modification of the flux intensities and spectra in the near field. We have shown that these devices are subject to surface recombinations and high carrier-density photogeneration. We have recently demonstrated experimentally that reasonable efficiencies and electrical power can be obtained with such near-field thermophotovoltaic devices when using low-energy bandgap cells. A second option for enhancing performance beyond the blackbody limit is thermophotonics, where the emitter is driven electrically without the need for external electrical power. We have shown that it can provide an interesting path for low-grade energy harvesting, especially in near-field configurations (1,2). In general, we are also interested in other prospective technologies combining thermal-energy transport and conversion with nanotechnology.
We are performing both experimental investigations (link to a basic presentation on thermal nanometrology, in French), with electro-thermal means as in scanning thermal microscopy and metal line-based deposited devices, and numerical studies, with the Boltzmann transport equation when particle transport is considered, or with wave equations such as the Maxwell ones or those associated to continuum elasticity. They have been or are performed in very close collaborations with friendly colleagues thanks to the support of various institutions.